TCB/fr

Language:

English • français

"TCB" est un type d'interpolation, acronyme de Tension, Continuité, Biais. Ce sont les trois caractéristiques qui définissent la forme de la courbe lorsque la valeur d'un paramètre interpolé est déterminé en fonction du temps.

Choisir le type d'interpolation TCB produit un courbe douce entre les Points de Passages adjacents, de la même manière que l'Outil Spline produit une courbe douce entre les vertexs limitrophes de la Spline. L'interpolation peut être contrôlé par quatre paramètres. Ce sont la "Tension", la "Continuité", le "Biais" ainsi que la "Tension Temporelle". En simplifiant ils contrôlent les choses suivantes :

Tension

La tension définit avec quelle raideur le Point de Passage seras pris pour cible (la quantité d'effet que l'opposé de tangente vas avoir). Cela est sensiblement comparable aux poignées d'une courbe de Bezier. Cette valeur définit de manière inverse la longueur que les poignées vont avoir.

• Une valeur élevée forcera le mouvement à être plus linéaire d'un Point de Passage à l'autre (les poignées deviennent plus courtes). Si elle est définit à la valeur 1.0, le résultat seras un changement de direction brusque. Si les autres paramètres ont la valeur par défaut 0, cela est équivalent à un mouvement linéaire (les poignées ont une longueur 0). En la définissant supérieure à 1.0 le résultat seras un mouvement courbe à l'approche de ce Point de Passage (les poignées sont misent à l'échelle dans une direction négative (elles sont échangées)).
• Des valeurs basses forceront l'objet à suivre la tangente (la poignée) de ce Point de Passage. Avec des valeurs très basses la plus part du mouvement suivras la tangente, comme si la tangente des poignées était très longue.

Continuité

Cette valeur définit comment la tangente est calculée. Cela peut aussi être comparé à la poignée d'un point d'une courbe de Bezier. Une valeur de 0 produiras des poignées symétriques (fusionnées), ce qui donneras une transition douce.

• En la réglant à -1.0 cela donneras un point de rebroussement, produisant une interpolation linéaire et un coin anguleux.
• En la réglant encore plus basse cela produira un rebroussement plus anguleux, ainsi le mouvement entrant et sortant deviendras de plus en plus symétrique.
• En réglant à une valeur supérieure que 0 cela donneras un effet similaire, mais les poignées ce déplaceront dans une direction opposée. Et donc l'interpolation débuteras depuis l'extérieur et ce dirigeras ensuite vers le Point de Passage.

Biais (Tendance)

Cette valeur définit qu'elle seras le segment, précédent et suivant le Point de Passage, qui auras le plus d'influence sur la tangente obtenue. Si le "Biais" est plus petit que 0 alors la tangente choisit seras celle qui est le plus orienté dans la direction entrante. Si la valeur est supérieur à 0 cela orienteras d'avantage dans la direction sortante.

Tension Temporelle

Par défaut, la vitesse d'un objet est constante lorsqu'elle passe à une même distante de Points de passages ayant un écart temps égal. Cette valeur peut être utilisé pour manipuler la vitesse du mouvement.

• Des valeurs plus élevées que 0 forceront l'objet à passer plus de temps à l'abords du Point de Passage. Cela produit un court ralentissement avant et après le Point de Passage. D'un autre point de vue, la vitesse augmenteras à l'approche du Point de Passage suivant.

Comme exemple illustratif, vous pouvez imaginer une balle située sur une petite montagne (le Point de Passage précédent), en dévalant la vallée elle vas prendre de la vitesse, en abordant une autre montagne plus haute, elle vas ralentir et parvenir au sommet (le Point de Passage modifié). Après cela, elle vas redescendre atteignant de nouveau une vitesse élevée dans la vallée, jusqu'à une autre petite montagne, perdant de la vitesse à mesure qu'elle se rapproche du sommet (le Point de Passage suivant).

• Des valeurs plus basses que 0 forceront l'objet à passer le Point de Passage rapidement. Cela produiras un ralentissement aux abords des Points de Passages précédent et suivant. Cela peut être comparé à une balle dévalant une vallée (l'exemple inverse du précédent).

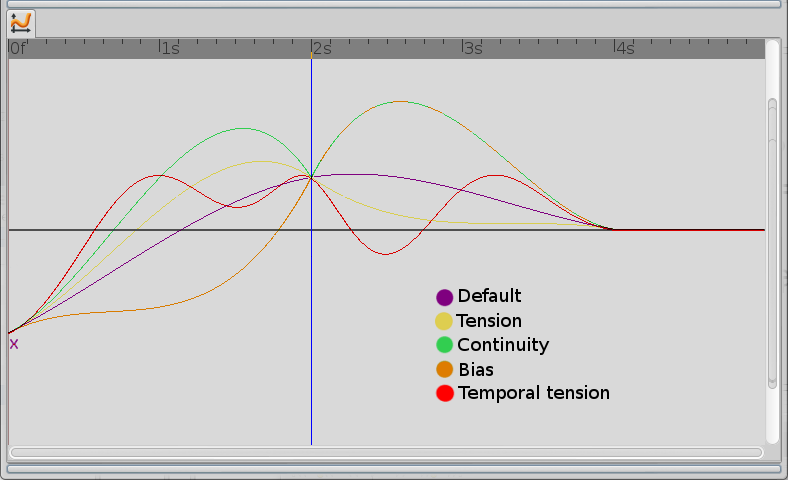
Example visuel

Toutes les trajectoires dans le Panneau Graphes (image composée avec Gimp)

Projet utilisé dans cette exemple : File:TCB-Example.sifz

Plus d'Informations

• Vous trouverez des discussions, en anglais, sur les mathématiques des TCB ici.
• Article wikipedia, en anglais, Kochanek–Bartels spline (également nommé TCB-Spline).
• Une ébauche d'information sur les courbes en infographie.

Language:

English • français