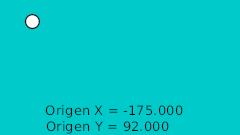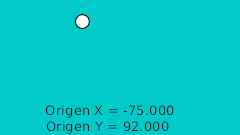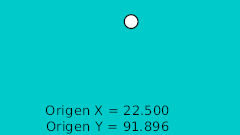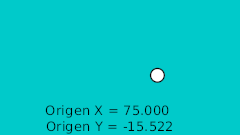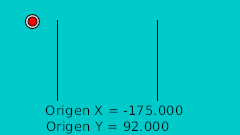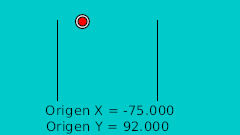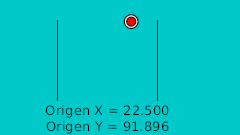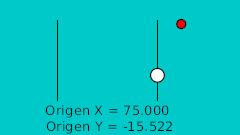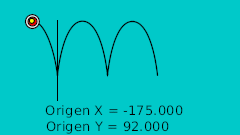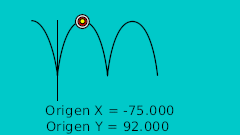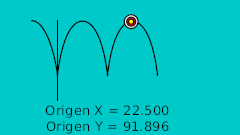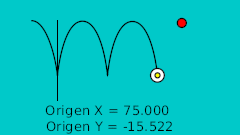Ball Bounce
m (Update screenshot progress) |
|||
| Line 57: | Line 57: | ||
This is the resulting graph for the manual approximation to the ball bounce. | This is the resulting graph for the manual approximation to the ball bounce. | ||
| − | {{l| | + | {{l|File:BallBounce-tuto-Manual-graph 0.63.06.png|800px}} |
The lower points are not peak points. To do that you need to insert more waypoints in intermediate places around the lower frame (20f). TRy it by your self with the attached file. | The lower points are not peak points. To do that you need to insert more waypoints in intermediate places around the lower frame (20f). TRy it by your self with the attached file. | ||
Revision as of 12:40, 21 April 2013
This tutorial explains how to create a bouncing ball animation, focusing on ball movement. Cartoon-like balls also have a very deformed shape while traveling and especially when they hit the ground. This could be covered in a second stage.
Contents
Different approximations for the same result
With Synfig there are four ways to create a bouncing ball:
- Do the bouncing ball manually. This involves creating several waypoints and adjust them to match a parabolic movement (in time and space).
- Use the interpolation parameters of the waypoints when they are set to TCB interpolation. This drastically reduces the amount of waypoints and also makes the timing of the bounces easier.
- Use the Link to spline feature. If you draw the path of a bouncing ball using a spline it is easy to make the ball follow the path even changing the bouncing speed.
- Create the mathematical equations to do that. Make several parabolic shots at the right place and the right time to simulate a bouncing ball. It would be a little tricky but probably should be the most accurate one.
Manual Ball Bounce
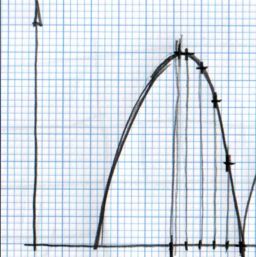
The rule to make the ball bounce manually is to draw in a paper the desired bounce. Then mark the horizontal line with regular intervals and match the curve intersection in vertical. See the image:
You can notice that having regular intervals in the horizontal axis gives irregular intervals to the vertical axis. It is due to the nature of the curve.
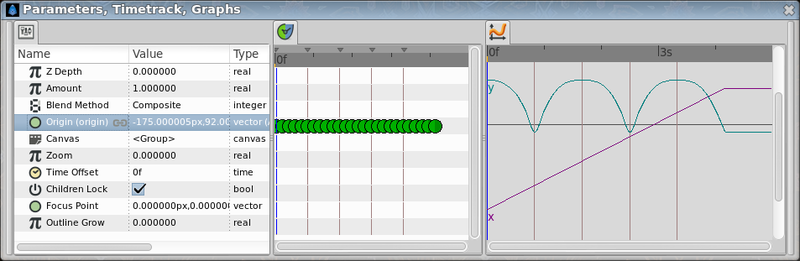
Once the points are located in a 2D grid then it can be drawn directly in Synfig doing use of the grid (F11). After drawing them we normalized the values to be completely symmetrical. That gives the following table:
| Time | X position | Y position | Comments |
| 0f | -175.0 | 92.0 | Highest point |
| 4f | -165.0 | 92.0 | |
| 8f | -155.0 | 81.118 | |
| 12f | -145.0 | 63.678 | |
| 16f | -135.0 | 29.479 | |
| 20f | -125.0 | -15.522 | Lower point |
| 24f | -115.0 | 29.479 | |
| 28f | -105.0 | 63.782 | |
| ... | ... |
You can see that the X position is increasing in steps of 10.0 and the Y position reproduces a parabolic curve.
To proceed with more than one bounce just duplicate the waypoints (place the cursor at the right place right click over the waypoint and duplicate) reproducing symmetrical movements. You should need to edit the X values manually to decrease by 10.0 for each new waypoint.
This is the resulting graph for the manual approximation to the ball bounce.
The lower points are not peak points. To do that you need to insert more waypoints in intermediate places around the lower frame (20f). TRy it by your self with the attached file.
The resulting animation and file are those ones.
File: Media:manual.sifz
Ball Bounce using waypoints interpolations
The TCB interpolation mode allows modify the Tension, Continuity, Bias, and Temporal Tension values of the waypoint. So you can create easily smooth or peak aproximation to the value of the valuenode in the waypoint position.
This time I would use the same values for the highest and lower points of the table before. But I won't use more than one waypoint for each extreme position. The rest of the curve would be done using the TCB parameters.
The table of waypoints gives this result:
| Time | X position | Y position | Comments |
| 0f | -175.0 | 92.0 | Highest point |
| 20f | -125.0 | -15.522 | Lower point |
| 40f | -75.0 | 92.0 | Highest point |
| 60f | -25.0 | -15.522 | Lower point |
| ... | ... |
As you can see the number of points is reduced drastically.
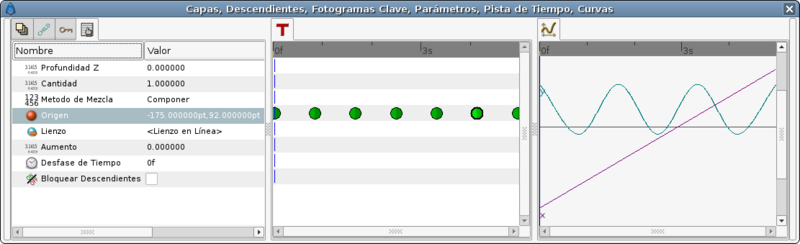
In you only use a default TCB interpolation it would give you a poor result. Look at the graph:
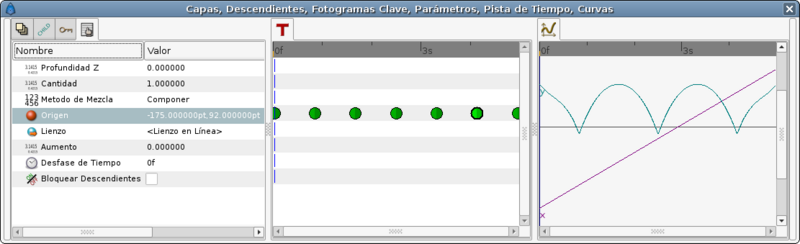
But if you edit the TCB parameters this is the result you obtain:
The TCB parameters are the following:
| Time | X position | Y position | Comments | Tension | Continuity | Bias | Temporal Tension |
| 0f | -175.0 | 92.0 | Highest point | 0.0 | 0.0 | 0.0 | 0.0 |
| 20f | -125.0 | -15.522 | Lower point | 0.0 | -2.2 | 0.0 | 0.0 |
| 40f | -75.0 | 92.0 | Highest point | 0.0 | 0.0 | 0.0 | 0.0 |
| 60f | -25.0 | -15.522 | Lower point | 0.0 | -2.2 | 0.0 | 0.0 |
| 80f | 25.0 | 92.0 | Highest point | 0.0 | 0.0 | 0.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
That's the resulting animation:
And the sample file: Media:waypoint-2.sifz
Notice that the curve at 0f and at 80f are not properly formed. It is due to the fact that the TCB parameters needs to belong to an intermediate waypoint to have effect. If the waypoint is extreme (the end or the beginning of the animation for the parameter it cannot modify the curve. To solve that you should split the X and Y coordinates of the Origin and apply a Ease In/Out interpolation to those Y coordinate and leave the X coordinate with the current interpolation. So please consider only the bounces between the two black vertical lines.
Notice also that you can make the highest point more flat increasing the Temporal Tension parameter (a good value can be 0.5). This would produce a deformation to the X coordinate so you need to separate both coordinates to do that. Try it by your self editing the attached file. I have left the highest point to have the default values.
Here is a comparison of both bounces a the same time.
With this approximation you can easily modify the Y coordinate of the highest points. The interpolation would take care of the rest. With the manual interpolation you should calculate all the x/y coordinates od the resulting curve for a lower bounce. You can record the values into a calculus sheet and just multiply the Y value by a reduction factor. Anyway you have to enter all the value pairs one by one.
Ball Bounce following a path
Before reading this section you should be familiar with Following a Spline tutorial.
The use of a path to perform the bounce has some advantages:
- You can see the complete ball bounces in one shot.
- You can make the ball rotate along the path (this would allow to make bounces of non round objects).
- You can make bounces to vertical, horizontal or any kind of walls you like. Just draw the path.
and some disadvantages:
- It is difficult to control the horizontal movement. It is due to the parameter that moves the object through the path is linked to the number of vertices of the path. If the path has five vertices and it is an open spline the parameter that defines the path has the following values when define each vertex: 0.0 for the first, 0.25 for the second, 0.5 for the third, 0.75 for the fourth and 1.0 for the fifth (and last) independent of the length of the spline section between vertices.
The first thing you have to do is define the path that the bouncing ball is going to describe. I've used the previous manual animation to draw this spline:
(You can notice that there are some missing tangents. It is due that I've linked the parallel tangents of the peak points of the path. It is more easy to setup because you only have to control two tangents to control all the tangents at the same time.)
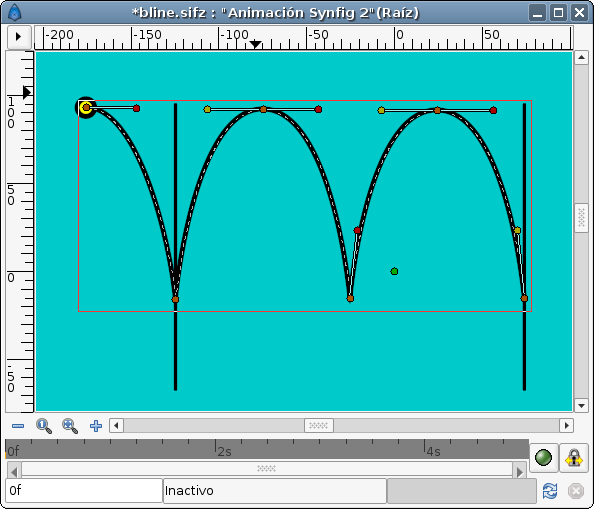
Once defined then create a circle or the ball you want to move and place it centered at the origin (0,0). I prefer that you group it and use the group layer origin parameter to make the animation. Once grouped select the spline you have created and the group layer of the grouped ball and select the Origin handle of the group layer. Then right click over the spline (avoiding any handle) and select "Link to Spline". You can see my green ball in the figure.
Once linked you can drag it and it will stick to the spline.
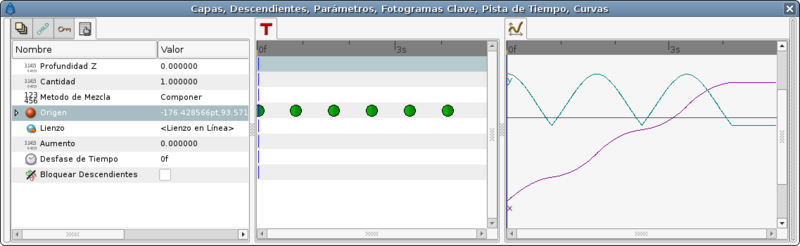
Now expand the Origin parameter of the group layer of the grouped ball and search for the Amount parameter. This parameter is the one you need to animate to move the ball over the spline.
Considering the example, the spline has 6 vertices and 5 spline sections. If you are following the tutorial try to set that parameter to 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 and you will see that the ball moves to each vertex. Now create the following waypoints:
| Time | Amount | Comments |
| 0f | 0.0 | Highest point |
| 20f | 0.2 | Lower point |
| 40f | 0.4 | Highest point |
| 60f | 0.6 | Lower point |
| 80f | 0.8 | Highest point |
| 100f | 1.0 | Lower point |
This coincides with the main waypoints of the last method we have seen. But look what's the result:
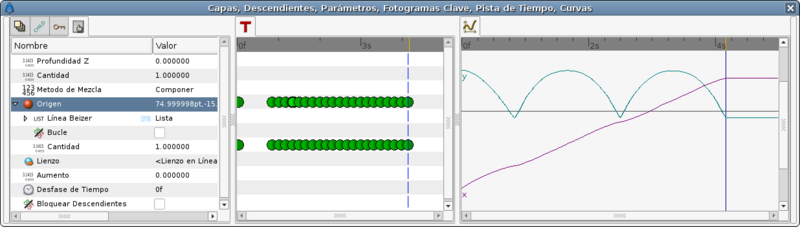
Its X movement graph looks ugly. It is not a straight line that means that the horizontal velocity is not constant. To solve that you have to insert more waypoints in the middle.
To do that I've uses the animation of the second method to try to match the position at regular intervals. This is the table I've needed.
| Time | Amount | Comments |
| 0f | 0.0 | Highest point |
| 20f | 0.2 | Lower point |
| 24f | 0.2626 | |
| 28f | 0.3085 | |
| 32f | 0.3463 | |
| 36f | 0.3741 | |
| 40f | 0.4 | Highest point |
| 44f | 0.4245 | |
| 48f | 0.4554 | |
| 52f | 0.4926 | |
| 56f | 0.5280 | |
| 60f | 0.6 | Lower point |
| 64f | 0.6629 | |
| 68f | 0.7075 | |
| 72f | 0.7445 | |
| 76f | 0.7783 | |
| 80f | 0.8 | Highest point |
| 84f | 0.8253 | |
| 88f | 0.8539 | |
| 92f | 0.8928 | |
| 96f | 0.9375 | |
| 100f | 1.0 | Lower point |
Now look to the graphs again and notice that the X travel is now a straight line.
This is the resulting animation and the sifz file.
The sample file: Media:bline.sifz
It is supposed that the small yellow ball should follow the red one all the time but you can see that is goes a little faster some times and a little slower other times. It is due to I need to use different times for the adjusting waypoints or add more of them.
Mathematical emulation
My approach is to imagine x and y movements as independent, so the x is simple (uniform rectilinear movement) and the y a little more complex. The first idea was to use the classical equations for acceleration (and gravity), but this would lead to need one equation per step (up-down or down-up). The ultimate idea is to use the sine function to describe the position at each timepoint, so... one equation would last forever!
Steps:
- Origin converted to composite
- X manualy animated to go linearly from left to right of the canvas: simple.
- Y converted to sine
- Sine Amplitude set to 1
- Sine DEG to time loop, and then:
- Timeloop link to 0 at 0 seconds and 180 at 1 second
- Timeloop duration: 1 second
- Rest timeloop parameters left to 0
I guess the result is almost correct although the shape of the curve is not perfect, but I don't know why. Upgrades might make the effect better, such as the ball bouncing less each time with a more complex function.
Anyone want to try? :)