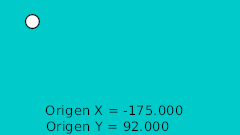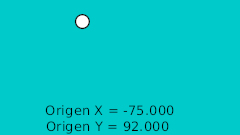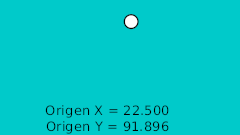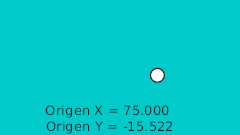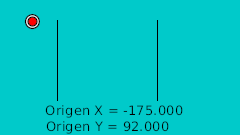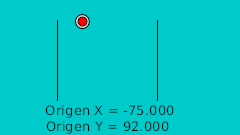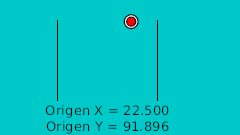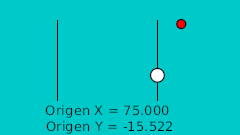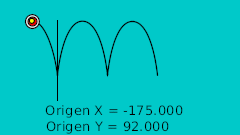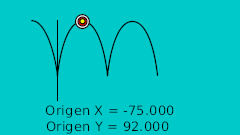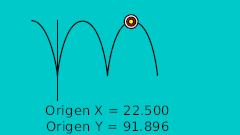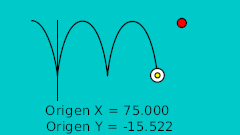Прыгающий мяч

Warning! This page contains outdated information. The release of Synfig Studio 0.64.0 introduced new terminology and this translated page needs to be updated according to original English text. You can help updating this page - see instructions here. Thank you!

warning end

В этой статье рассказывается о том как создать анимацию с прыгающим мячом. Мячи в мультиках обычно имеют достаточно причудливую форму когда двигаются и особенно когда ударяются об землю, но заниматься созданием таких деформаций мы будем в следующий раз, а сейчас рассмотрим способы создания самого движения мяча в пространстве.

Несколько разных способов достичь результата

Есть четыре способа создать прыгающий мяч используя Synfig:

1. Сделать прыгающий мяч вручную, это потребует создания нескольких фиксаторов которые надо расположить так чтобы положение мяча совпадало с параболической траекторией его движения (во времени и пространстве).
2. Используя параметр интерполяции фиксаторов, когда они установлены в режим TCB interpolation. Это значительно уменьшает количество необходимых фиксаторов и делает тайминг движения мяча на много проще.
3. Используя привязывание к кривой, если вы нарисуете путь по которому должен двигаться мяч используя кривую BLine, то достаточно просто сделать так чтобы мяч следовал вдоль кривой и даже изменял свою скорость во время движения.
4. Создать математическое уравнение описывающие движение мяча, это достаточно сложный способ но именно он должен оказаться самым точным из всех.

Создаём прыгающий мяч вручную

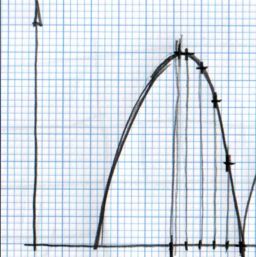
Принцип создания прыгающего мяча вручную заключается в том чтобы нарисовать желаемую кривую траектории на бумаге, а за тем прочертить от горизонтальной оси линии пересекающие кривую траектории с одинаковыми промежутками между собой. Примерно как на этом рисунке:

Вы можете заметить что одинаковые промежутки на горизонтальной оси дают на вертикальной оси не одинаковые промежутки, это нормально так как проистекает из природы кривой.

Определив точки пересечения с кривой в двух измерениях мы можем перенести их в Synfig напрямую, используя для этого сетку. Нарисовав их мы исправляем значения координат так чтобы они были полностью симметричны, что наглядно показано на этой таблице:

Время	X	Y	Коментарий
0f	-175.0	92.0	Высшая точка
4f	-165.0	92.0
8f	-155.0	81.118
12f	-145.0	63.678
16f	-135.0	29.479
20f	-125.0	-15.522	Низшая точка
24f	-115.0	29.479
28f	-105.0	63.782
...	...

Вы можете видеть что позиция Х возрастает с шагом в 10.0, а позиция Y воспроизводит параболическую траекторию кривой.

Чтобы получить большее количество прыжков просто скопируйте фиксаторы. Вам также придётся отредактировать значения Х вручную чтобы они возрастали на 10.0 на каждом новом фиксаторе.

To proceed with more than one bounce just duplicate the waypoints (place the cursor at the right place right click over the waypoint and duplicate) reproducing symmetrical movements. You should need to edit the X values manually to decrease by 10.0 for each new waypoint.

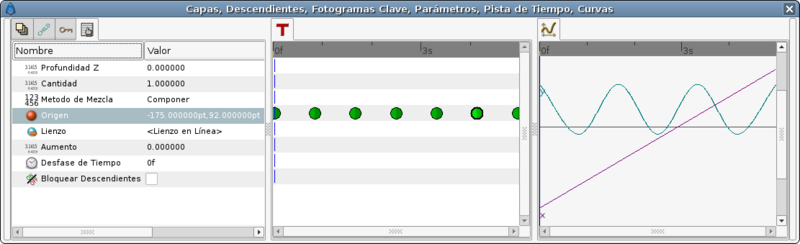
This is the resulting graph for the manual approximation to the ball bounce.

The lower points are not peak points. To do that you need to insert more waypoints in intermediate places around the lower frame (20f). TRy it by your self with the attached file.

The resulting animation and file are those ones.

File: Media:manual.sifz

Ball Bounce using waypoints interpolations

The TCB interpolation mode allows modify the Tension, Continuity, Bias, and Temporal Tension values of the waypoint. So you can create easily smooth or peak aproximation to the value of the valuenode in the waypoint position.

This time I would use the same values for the highest and lower points of the table before. But I won't use more than one waypoint for each extreme position. The rest of the curve would be done using the TCB parameters.

The table of waypoints gives this result:

Time	X position	Y position	Comments
0f	-175.0	92.0	Highest point
20f	-125.0	-15.522	Lower point
40f	-75.0	92.0	Highest point
60f	-25.0	-15.522	Lower point
...	...

As you can see the number of points is reduced drastically.

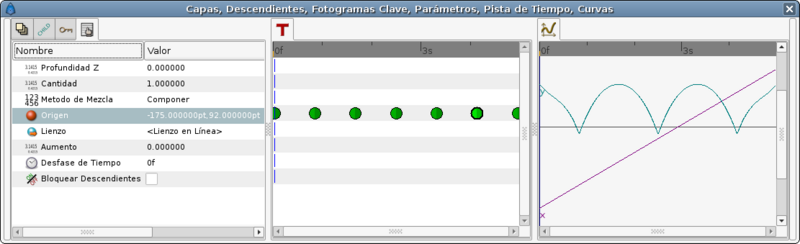
In you only use a default TCB interpolation it would give you a poor result. Look at the graph:

But if you edit the TCB parameters this is the result you obtain:

The TCB parameters are the following:

Time	X position	Y position	Comments	Tension	Continuity	Bias	Temporal Tension
0f	-175.0	92.0	Highest point	0.0	0.0	0.0	0.0
20f	-125.0	-15.522	Lower point	0.0	-2.2	0.0	0.0
40f	-75.0	92.0	Highest point	0.0	0.0	0.0	0.0
60f	-25.0	-15.522	Lower point	0.0	-2.2	0.0	0.0
80f	25.0	92.0	Highest point	0.0	0.0	0.0	0.0
...	...	...	...	...	...	...	...

That's the resulting animation:

And the sample file: Media:waypoint-2.sifz

Notice that the curve at 0f and at 80f are not properly formed. It is due to the fact that the TCB parameters needs to belong to an intermediate waypoint to have effect. If the waypoint is extreme (the end or the beginning of the animation for the parameter it cannot modify the curve. To solve that you should split the X and Y coordinates of the Origin and apply a Ease In/Out interpolation to those Y coordinate and leave the X coordinate with the current interpolation. So please consider only the bounces between the two black vertical lines.

Notice also that you can make the highest point more flat increasing the Temporal Tension parameter (a good value can be 0.5). This would produce a deformation to the X coordinate so you need to separate both coordinates to do that. Try it by your self editing the attached file. I have left the highest point to have the default values.

Here is a comparison of both bounces a the same time.

With this approximation you can easily modify the Y coordinate of the highest points. The interpolation would take care of the rest. With the manual interpolation you should calculate all the x/y coordinates od the resulting curve for a lower bounce. You can record the values into a calculus sheet and just multiply the Y value by a reduction factor. Anyway you have to enter all the value pairs one by one.

Ball Bounce following a path

Before reading this section you should be familiar with Doc:Following_a_BLine/ru tutorial.

The use of a path to perform the bounce has some advantages:

• You can see the complete ball bounces in one shot.
• You can make the ball rotate along the path (this would allow to make bounces of non round objects).
• You can make bounces to vertical, horizontal or any kind of walls you like. Just draw the path.

and some disadvantages:

• It is difficult to control the horizontal movement. It is due to the parameter that moves the object through the path is linked to the number of vertices of the path. If the path has five vertices and it is an open Bline the parameter that defines the path has the following values when define each vertex: 0.0 for the first, 0.25 for the second, 0.5 for the third, 0.75 for the fourth and 1.0 for the fifth (and last) independent of the length of the Bline section between vertices.

The first thing you have to do is define the path that the bouncing ball is going to describe. I've used the previous manual animation to draw this Bline:

(You can notice that there are some missing tangents. It is due that I've linked the parallel tangents of the peak points of the path. It is more easy to setup because you only have to control two tangents to control all the tangents at the same time.)

Once defined then create a circle or the ball you want to move and place it centered at the origin (0,0). I prefer that you encapsulate it and use the paste canvas origin parameter to make the animation. Once encapsulated select the bline you have created and the paste canvas of the encapsulated ball and select the Origin duck of the paste canvas. Then right click over the bline (avoiding any duck) and select "Link to Bline". You can see my green ball in the figure.

Once linked you can drag it and it will stick to the bline.

Now expand the Origin parameter of the paste canvas layer of the encapsulated ball and search for the Amount parameter. This parameter is the one you need to animate to move the ball over the Bline.

Considering the example, the bline has 6 vertices and 5 bline sections. If you are following the tutorial try to set that parameter to 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 and you will see that the ball moves to each vertex. Now create the following waypoints:

Time	Amount	Comments
0f	0.0	Highest point
20f	0.2	Lower point
40f	0.4	Highest point
60f	0.6	Lower point
80f	0.8	Highest point
100f	1.0	Lower point

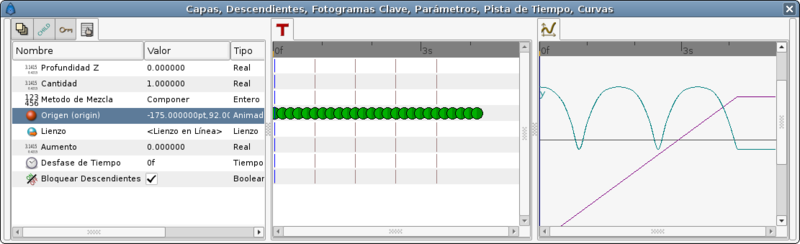
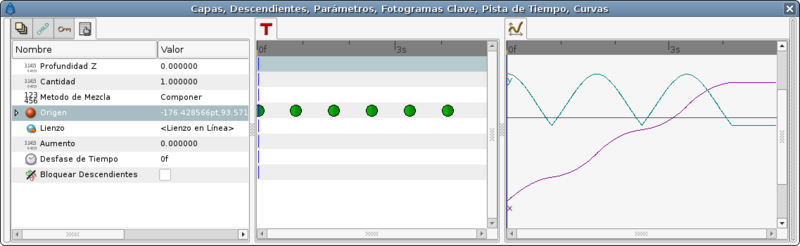
This coincides with the main waypoints of the last method we have seen. But look what's the result:

Its X movement graph looks ugly. It is not a straight line that means that the horizontal velocity is not constant. To solve that you have to insert more waypoints in the middle.

To do that I've uses the animation of the second method to try to match the position at regular intervals. This is the table I've needed.

Time	Amount	Comments
0f	0.0	Highest point
20f	0.2	Lower point
24f	0.2626
28f	0.3085
32f	0.3463
36f	0.3741
40f	0.4	Highest point
44f	0.4245
48f	0.4554
52f	0.4926
56f	0.5280
60f	0.6	Lower point
64f	0.6629
68f	0.7075
72f	0.7445
76f	0.7783
80f	0.8	Highest point
84f	0.8253
88f	0.8539
92f	0.8928
96f	0.9375
100f	1.0	Lower point

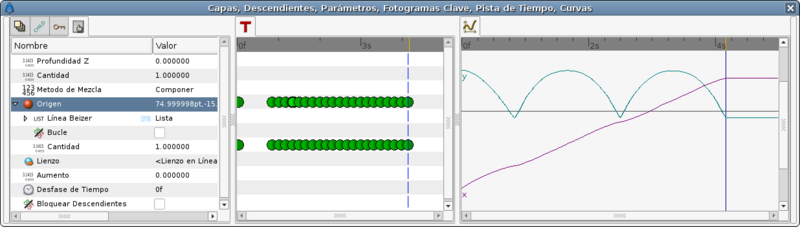
Now look to the graphs again and notice that the X travel is now a straight line.

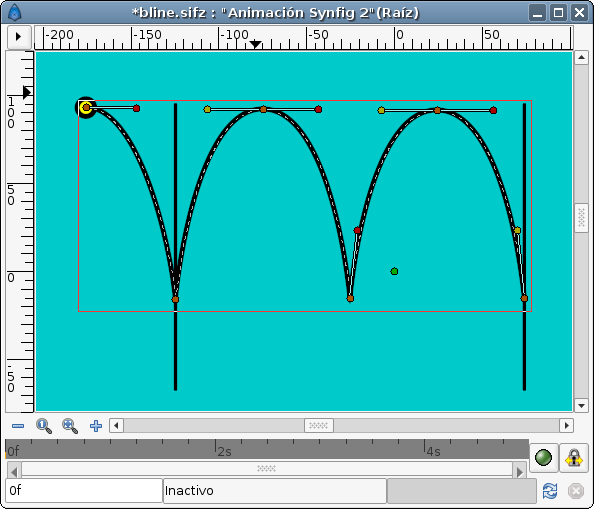
This is the resulting animation and the sifz file.

The sample file: Media:bline.sifz

It is supposed that the small yellow ball should follow the red one all the time but you can see that is goes a little faster some times and a little slower other times. It is due to I need to use different times for the adjusting waypoints or add more of them.

Mathematical emulation

Anyone want to try? :)

Conclusions