Dev talk:Bone Layer
Deleted Section. Kept for future references
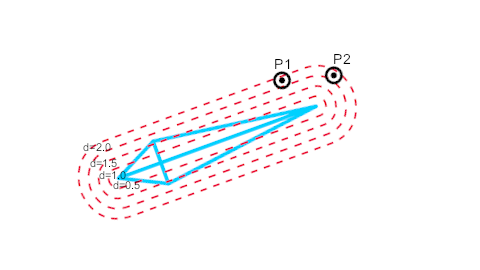
The calculation of the weight w is calculated based on the distance d of the point P to the bone according to this diagram:
Notice how the point P1 is located at same distance d to the bone than the point P2.
There are possibles formulation to calculate w based on d values but some initial are these:
- Point is Fixed Bind to the Bone: Bone has always the same weight regardless the distance form the bone.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle w=1 }
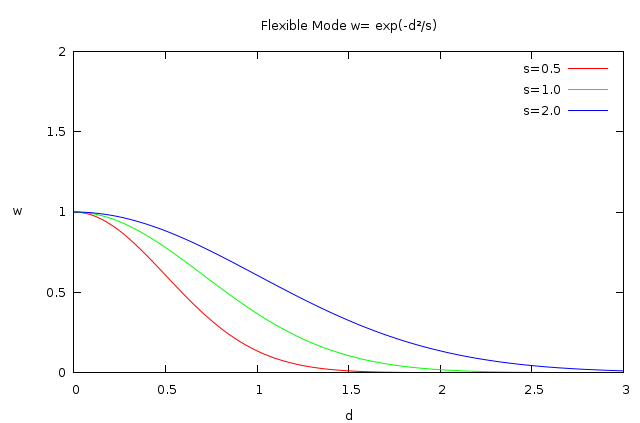
- Point Flexible Binded to the Bone: that means that the bone has influence to the point always but it decreases exponentially to with the distance d². Here is a new parameter called s (strength). it can modify the weight function of the bone with the distance d.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle w=e^{-\frac{d^2}{s}} }
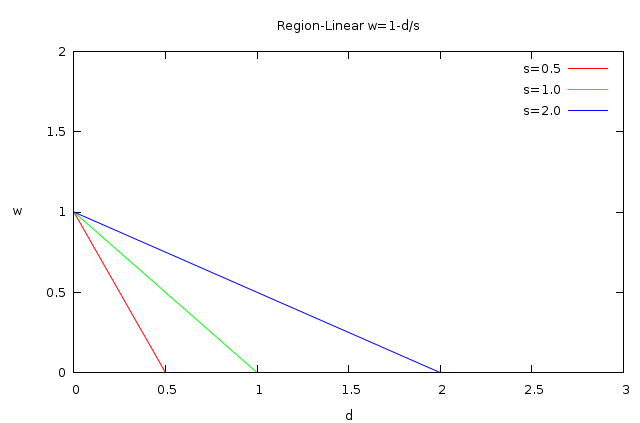
- Point Region-Linear Binded to the Bone: that means that the bone has influence to the point only inside a certain region and it decreases linearly from w=1 when d=0 w=0 when d=s.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle w=1-\frac{d}{s} }
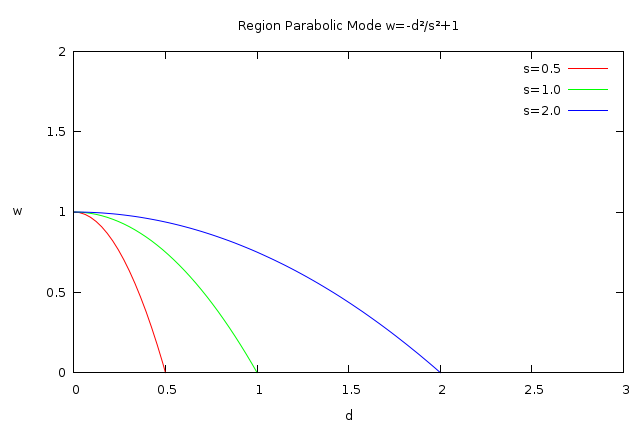
- Point Region-Parabolic Binded to the Bone: that means that the bone has influence to the point only inside a certain region and it decreases parabolic from w=1 when d=0 w=0 when d=s.
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle w=1-\frac{d^2}{s^2} }
Rewinding to the concept introduced in the previous section (the amount of influence of each bone called w) you can remember that it was calculated based on the "distance" (d) of the point from the bone and the "strength" (s) of the bone. See the graphics before. As you can see, there are some of the possible w definitions that has a value of w=0 for d>s. It means that the weight of that bone over this point is null and doesn't contribute to the movement of the point resulting of the influence of the bone(s).
That possibility (w=0) triggers two questions:
1) What happen if all the bones has the weight w=0 for a certain point?.
2) If the point can move additionally to the bone movement influence, can the distance (d) to the bone produce that the weight (w) becomes w=0 and the point is out of influence from that bone? If the point goes out of all the bones influence regions it triggers the question 1).
Answer to 2):
We are assuming that the distance (d) from the point to the bone is calculated based on the current distance from the point to the bone. That's not necessarily true. We can have a kind of "static" point that defines the relative position of the point from the bone for the distance (d) calculation and then apply the weight to the bone(s) influence matrix regardless the current point position give by the sum of (a) + (b) (explained before).
Let's call that relative position Q. That "static" position can be given in two ways: in coordinates relative to each bone (a Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle Q_i } for each bone i) or a single absolute coordinate Q value for the point and the distances (d) for each bone is calculated based on an static set of bone positions (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle B_s } ). In any case the weights (w) need some "static" values to get the information from. I type "static" and not static (without quotes) because I think that it can be an animatable value (but usually it isn't).
Discussion by rubikcube
- I think the image has one small mistake: shouldn't Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://api.formulasearchengine.com/v1/":): {\displaystyle \alpha} be from the horizontal axis to the bone's axis? At the moment it's from the horizontal to the connection line (OO').
I'm referring to http://synfig.org/Image:Bonesimulation.png
--Rubikcube 11:06, 27 November 2008 (EST)