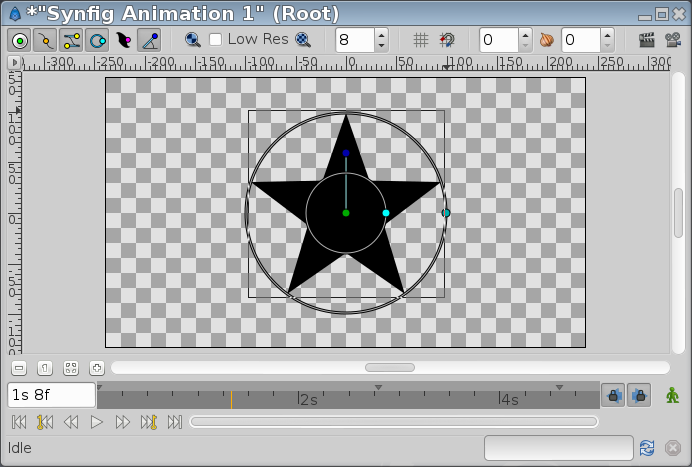
Star Layer
Contents
About Star Layers
A "Star Layer" is a geometric object that is made by the filling the region resulting from connecting the points of two concentric circles with straight lines. The number of points on which the circles are divided defines the number of peaks of the star. The points over the circles are spread regularly over both circles but one of them has the points rotated N/360/2 degrees from the other circle (being N the number of peaks or points).
Parameters of Star Layers
The parameters of the star layers are:
| Name | Value | Type |
| 0.000000 | real | |
| 1.000000 | real | |
| Composite | integer | |
|
|
color | |
| 0.500000u,0.000000u | vector | |
|
|
bool | |
|
|
bool | |
| 0.500000u | real | |
| Fast Gaussian Blur | integer | |
| Non Zero | integer | |
| 1.500000u | real | |
| 0.500000u | real | |
| 0.00 | angle | |
| 5 | integer | |
|
|
bool |
The parameters of the star layers are the same as the majority of the shape-like objects but it has specific parameters for its own properties.
Outer Radius
Defines the radius of the circle where the peaks of the star lay.
Inner Radius
Defines the radius of the circle where the valleys of the star lay.
Angle
Is the rotation angle for the first peak of the star. Its default value is 90 degrees.
Points
Defines the number of divisions done in the circles and therefore the number of points and peaks in the star.
Playing Around
Crazy Radii
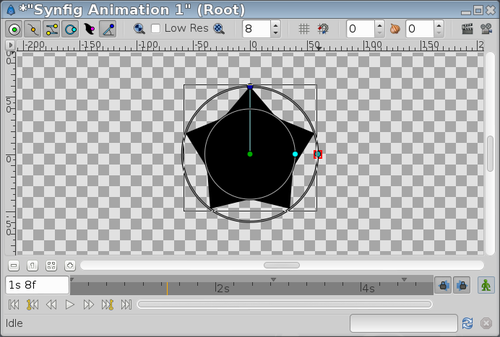
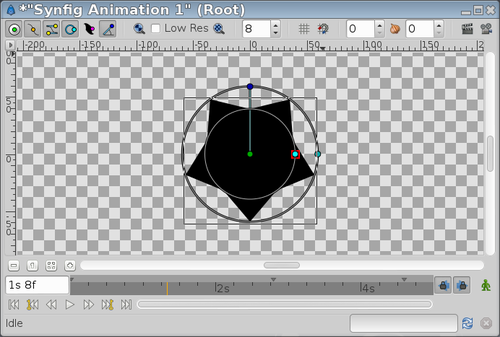
The "Outer Radius" shouldn't be greater than "Inner Radius". It only changes the star's orientation:
| Inner Radius = 40; Outer Radius = 60 | Inner Radius = 60; Outer Radius = 40 |
 |
|
You can also play with negative values:
| Inner Radius = -40; Outer Radius = 60 | Inner Radius = 40; Outer Radius = -60 |
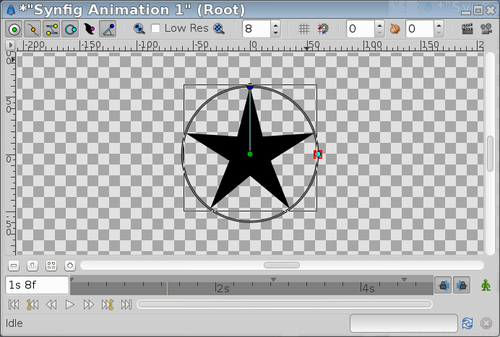 |
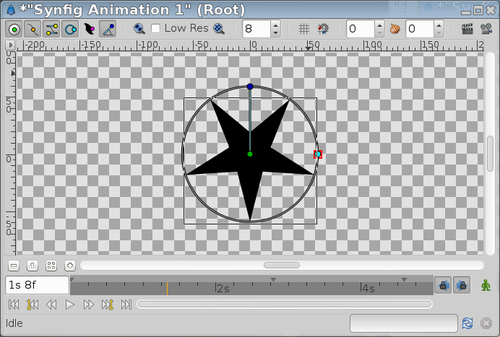
|
Winding Style Hacks
You can even play with the Winding Style Parameter and negative values to obtain some effects:
| Inner Radius = 40; Outer Radius = -60; WS=even/odd | Inner Radius = -40; Outer Radius = 60; WS=even/odd |
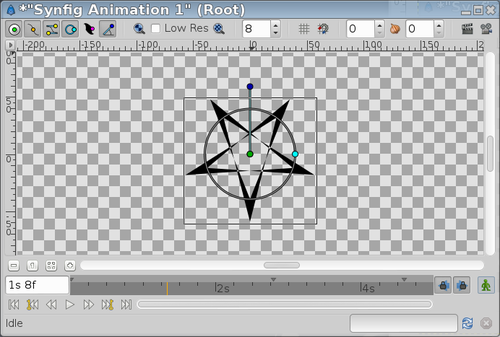 |
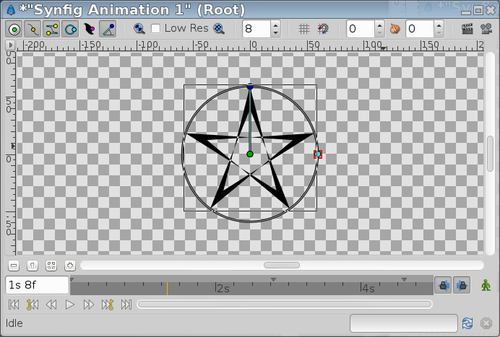
|
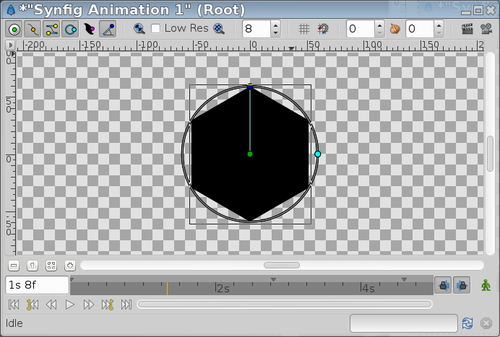
Regular 2N-sided Polygons
Also you can link both radii to create a 2*N sided regular polygon, where N is the number of points (3 points for this case (six sides)):
| Language: |
English |