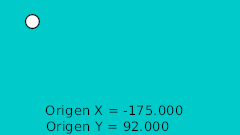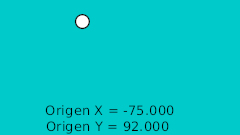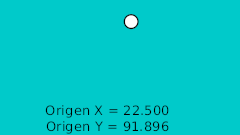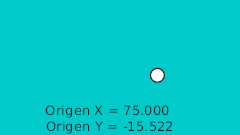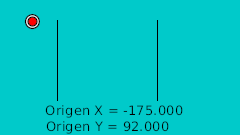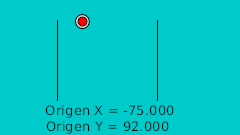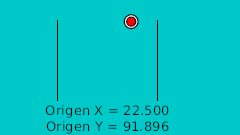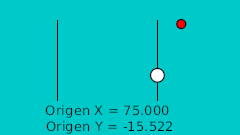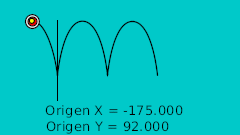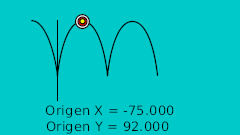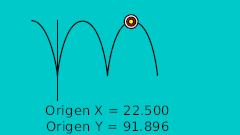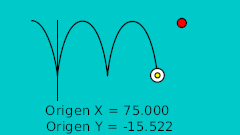Difference between revisions of "Doc:Ball Bounce/fr"
m (→Ball Bounce using waypoints interpolations: translation progress) |
m (addition of the English tutorial in french version) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
{{Category|Tutorials}} | {{Category|Tutorials}} | ||
{{Category|Tutorials Intermediate}} | {{Category|Tutorials Intermediate}} | ||
| + | {{NewTerminology}} | ||
<!-- Page info end --> | <!-- Page info end --> | ||
| Line 72: | Line 73: | ||
Le mode d'interpolation {{l|TCB}} permet de modifier les valeurs de {{literal|Tension}}, {{literal|Continuité}}, {{literal|Biais}} et de {{literal|Tension Temporelle}} du points de passage. Vous pouvez ainsi créer facilement une approximation douce ou pointue du {{l|ValueNode}} à la position du point de passage. | Le mode d'interpolation {{l|TCB}} permet de modifier les valeurs de {{literal|Tension}}, {{literal|Continuité}}, {{literal|Biais}} et de {{literal|Tension Temporelle}} du points de passage. Vous pouvez ainsi créer facilement une approximation douce ou pointue du {{l|ValueNode}} à la position du point de passage. | ||
| − | Cette fois | + | Cette fois-ci, je vais utiliser des valeurs identiques pour les points supérieurs et inférieurs de la table précédente. Mais je ne veux pas utiliser plus d'un point de passage pour chaque extrémités. Le reste de la courbe seras réalisée en utilisant des paramètres TCB. |
La table des points de passages ressemble donc à ceci : | La table des points de passages ressemble donc à ceci : | ||
| Line 182: | Line 183: | ||
This coincides with the main waypoints of the last method we have seen. But look what's the result: | This coincides with the main waypoints of the last method we have seen. But look what's the result: | ||
| − | {{l|Image: | + | {{l|Image:BallBounce-tuto-Spline-track1 0.63.06.png|800px}} |
Its X movement graph looks ugly. It is not a straight line that means that the horizontal velocity is not constant. To solve that you have to insert more waypoints in the middle. | Its X movement graph looks ugly. It is not a straight line that means that the horizontal velocity is not constant. To solve that you have to insert more waypoints in the middle. | ||
| Line 239: | Line 240: | ||
Now look to the graphs again and notice that the X travel is now a ''straight'' line. | Now look to the graphs again and notice that the X travel is now a ''straight'' line. | ||
| − | {{l|Image: | + | {{l|Image:BallBounce-tuto-Spline-track2 0.63.06.png|800px}} |
This is the resulting animation and the sifz file. | This is the resulting animation and the sifz file. | ||
| Line 247: | Line 248: | ||
The sample file: {{l|Media:bline.sifz}} | The sample file: {{l|Media:bline.sifz}} | ||
| − | It is supposed that the small yellow ball should follow the red one all the time but you can see that is goes a little faster some times and a little slower other times. It is due to I need to use different times for the adjusting waypoints or add more of them. | + | It is supposed that the small yellow ball should follow the red one all the time but you can see that is goes a little faster some times and a little slower other times. It is due to I need to use different times for the adjusting waypoints or add more of them. |
| − | + | ||
== Mathematical emulation == | == Mathematical emulation == | ||
| + | |||
| + | My approach is to imagine x and y movements as independent, so the x is simple (uniform rectilinear movement) and the y a little more complex. The first idea was to use the classical equations for acceleration (and gravity), but this would lead to need one equation per step (up-down or down-up). The ultimate idea is to use the sine function to describe the position at each timepoint, so... one equation would last forever! | ||
| + | |||
| + | Steps: | ||
| + | * Origin converted to composite | ||
| + | * X manualy animated to go linearly from left to right of the canvas: simple. | ||
| + | * Y converted to sine | ||
| + | * Sine Amplitude set to 1 | ||
| + | * Sine DEG to time loop, and then: | ||
| + | * Timeloop link to 0 at 0 seconds and 180 at 1 second | ||
| + | * Timeloop duration: 1 second | ||
| + | * Rest timeloop parameters left to 0 | ||
| + | |||
| + | I guess the result is almost correct although the shape of the curve is not perfect, but I don't know why. Upgrades might make the effect better, such as the ball bouncing less each time with a more complex function. | ||
| + | |||
Anyone want to try? :) | Anyone want to try? :) | ||
Latest revision as of 19:48, 3 March 2016
Cette page est en cours de traduction, soyez patient ou contribuez !.
Voici un tutoriel qui vous permettra de réaliser le rebond d'une balle en se focalisant sur son mouvement. Les balles dans les dessins dessinées subissent une grande déformation de leur forme, et encore plus lorsqu'elles touchent le sol. Cela pourrait être traitée dans une seconde étape.
Contents
Approximations différentes pour un résultat identique
Avec Synfig, il y à quatre façons de réaliser le rebond d'une balle.
- En créant le rebond manuellement. Cela implique de créer plusieurs Points de Passages et de les ajuster pour correspondre à un mouvement parabolique (en temps et en trajectoire).
- En utilisant les paramètres d'interpolations TCB des points de passages. Cela réduit considérablement la quantité de points de passages et aussi rend le tempo du rebond plus simple.
- En utilisant la fonctionnalité de Link to Spline. Si vous dessinez la trajectoire d'une balle qui rebondit en utilisant une Spline, il sera assez simple de faire suivre à la balle le chemin désiré, et même changer sa vitesse.
- La quatrième et dernière façon consiste à utiliser des équations mathématiques pour le faire. Il suffit de simuler plusieurs tirs paraboliques au bon endroit et au bon moment afin de créer le rebond. Cela est plus délicat, mais plus précis.
Rebond de Balle Manuel
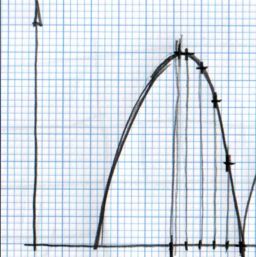
La méthode pour réaliser un rebond de balle manuel, est de dessiner le rebond voulu sur papier. Puis, depuis l'axe horizontal reportez à un intervalle régulier l'intersection de la courbe sur l'axe vertical. Voyez l'image suivante :
Vous pouvez remarquer que, partant d'un intervalle régulier sur l'axe horizontal cela résulte à un intervalle irrégulier sur l'axe vertical. Cela est du au type de la courbe.
Une fois les points situés sur une grille 2D, ils peuvent être directement dessinés dans Synfig en utilisant la grille (F11). Après les avoir dessinés, nous avons normalisé les valeurs afin d'être totalement symétrique. Cela donne la table suivante:
| Temps | Position X | Position Y | Commentaires |
| 0f | -175.0 | 92.0 | Point le plus haut |
| 4f | -165.0 | 92.0 | |
| 8f | -155.0 | 81.118 | |
| 12f | -145.0 | 63.678 | |
| 16f | -135.0 | 29.479 | |
| 20f | -125.0 | -15.522 | Point le plus bas |
| 24f | -115.0 | 29.479 | |
| 28f | -105.0 | 63.782 | |
| ... | ... |
Vous pouvez remarquer que la position X augmente par palier de 10.0 et que la Y position reproduit la courbe parabolique.
Afin de produire plus d'un rebond, dupliquez les points de passages (positionnez le curseur de temps à l'endroit voulu, cliquez droit sur le point de passage et sélectionnez "Dupliquer") afin de reproduire de mouvement symétrique. Vous aurez ensuite besoin de réduire manuellement les valeurs X de 10.0 pour chacun des nouveaux points de passages.
Voici le graphique correspondant à la méthode manuel du rebond d'une balle.
Les points bas ne sont pas pointues. Pour qu'ils le soient vous devrez ajouter des points des passages intermédiaires autour de l'image basse (20f). Testez par vous même en utilisant le fichier joint.
Voici l'animation résultante ainsi que le fichier de projet.
Projet : Media:manual.sifz
Rebond de Balle en utilisant l'interpolation des points de passages
Le mode d'interpolation TCB permet de modifier les valeurs de "Tension", "Continuité", "Biais" et de "Tension Temporelle" du points de passage. Vous pouvez ainsi créer facilement une approximation douce ou pointue du Noeud de Valeur à la position du point de passage.
Cette fois-ci, je vais utiliser des valeurs identiques pour les points supérieurs et inférieurs de la table précédente. Mais je ne veux pas utiliser plus d'un point de passage pour chaque extrémités. Le reste de la courbe seras réalisée en utilisant des paramètres TCB.
La table des points de passages ressemble donc à ceci :
| Temps | Position X | Position Y | Commentaires |
| 0f | -175.0 | 92.0 | Point Supérieur |
| 20f | -125.0 | -15.522 | Point Inférieur |
| 40f | -75.0 | 92.0 | Point Supérieur |
| 60f | -25.0 | -15.522 | Point Inférieur |
| ... | ... |
Comme vous pouvez le noter, le nombre de points à été réduit de manière drastique.
Si vous utilisez uniquement l'interpolation TCB par défaut, cela vous donneras un résultat pas terrible. Jetons un oeil au graphique :
Mais si vous changez les paramètres TCB voici le résultat que vous pouvez obtenir :
Les paramètres TCB sont les suivants :
| Temps | Position X | Position Y | Commentaires | Tension | Continuité | Biais | Tension Temporelle |
| 0f | -175.0 | 92.0 | Point Supérieur | 0.0 | 0.0 | 0.0 | 0.0 |
| 20f | -125.0 | -15.522 | Point Inférieur | 0.0 | -2.2 | 0.0 | 0.0 |
| 40f | -75.0 | 92.0 | Point Supérieur | 0.0 | 0.0 | 0.0 | 0.0 |
| 60f | -25.0 | -15.522 | Point Inférieur | 0.0 | -2.2 | 0.0 | 0.0 |
| 80f | 25.0 | 92.0 | Point Supérieur | 0.0 | 0.0 | 0.0 | 0.0 |
| ... | ... | ... | ... | ... | ... | ... | ... |
Ce qui donne comme animation :
Et le fichier du projet : Media:waypoint-2.sifz
Vous pouvez remarquer que la courbe à 0f et à 80f n'est pas bien formé. C'est du au fait que les paramètres TCB ont besoin de faire partis à une point de passage intermédiaire pour faire effet. Si le point de passage est à une extrémité (pour la fin ou le début de l'animation il ne peut pas modifier la courbe). Pour résoudre cela il faut séparer la coordonnée X et Y de l'"Origine" et appliquer une interpolation Ease In/Out à la coordonnée Y et laisser la coordonnée X avec l'interpolation actuelle. Donc, dans l'exemple, il faut considérer uniquement les rebonds compris entre les deux lignes verticales noirs.
Vous pouvez aussi rendre le point supérieur plus plat en augmentant la Tension Temporelle (0.5 peut être un bonne valeur). Cela produiras une déformation de la coordonnée X, donc vous avez besoin de séparer les deux coordonnées pour faire cela. Testez par vous même en jouant avec le fichier attaché. Le point supérieur à été laissé à la valeur par défaut.
Voici une comparaison des deux rebonds en même temps.
Avec cette approximation, vous pouvez facilement modifier la coordonnée Y du point supérieur. L'interpolation feras le reste pour vous. Avec l'interpolation manuelle vous devriez calculer toutes les coordonnées X/Y de la courbe pour obtenir un rebond plus bas. C'est possible de saisir les valeurs dans une feuille de calcul et multipliez la valeur Y par un facteur de réduction, mais vous aurez besoin de saisir les valeurs une par une à la main.
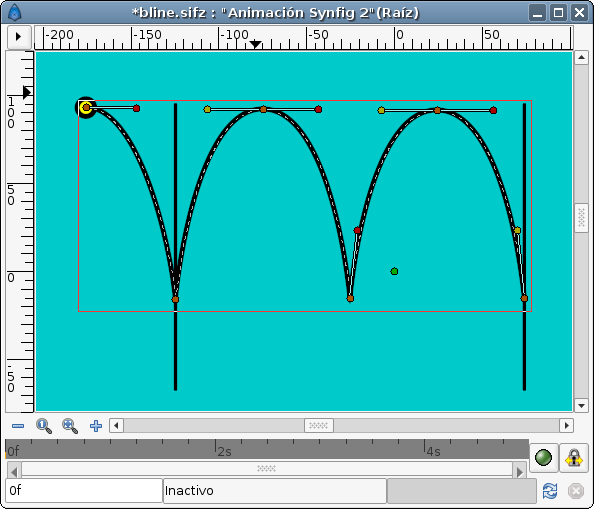
Ball Bounce following a path
To follow this section you should consider read the Follow a Bline tutorial. It makes use of that feature.
The use of a path to perform the bounce have some advantages.
- You can see the complete ball bounces in one shot.
- You can make the ball rotate along the path (this would allow make bounces of non rounded things).
- You can make bounces to vertical,horizontal or any kind of walls you like. Just draw the path.
It has some disadvantages:
- It is difficult to control the horizontal movement. It is due to the paramter that moves the object through the path is linked to the number of vertices vertices of the path. If the path have five vertices and it is an open Bline the parameter that defines the path has the following values when define each vertex: 0.0 for the first, 0.25 for the second, 0.5 for the third, 0.75 for the fourth and 1.0 for the fifth (and last) independent of the length of the Bline section between vertices.
The first thing you have to do is define the path that the bouncing ball is going to describe. I've used the previous manual animation to draw this Bline:
(You can notice that there are some missing tangents. It is due that I've linked the parallel tangents of the peak points of the path. It is more easy to setup because you only have to control two tangents to control all the tangents at the same time.)
Once defined then create a circle or the ball you want to move and place it centred at the origin (0,0). I prefer that you encapsulate it and use the paste canvas origin parameter to make the animation. Once encapsulated select the bline you have created and the paste canvas of the encapsulated ball and select the Origin duck of the paste canvas. Then make right click over the bline (avoiding any duck) and select "Link to Bline". You can see my green ball in the figure.
Once linked you can drag it and it would be stick to the bline.
Now expand the Origin parameter of the paste canvas layer of the encapsulated ball and search for the Amount parameter. This parameter is the parameter you need to animate to move the ball over the Bline.
Considering the example, the bline has 6 vertices and 5 bline sections. If you are following the tutorial try to set that parameter to 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 and you will see that the ball moves to each vertex. Now create the following waypoints:
| Time | Amount | Comments |
| 0f | 0.0 | Highest point |
| 20f | 0.2 | Lower point |
| 40f | 0.4 | Highest point |
| 60f | 0.6 | Lower point |
| 80f | 0.8 | Highest point |
| 100f | 1.0 | Lower point |
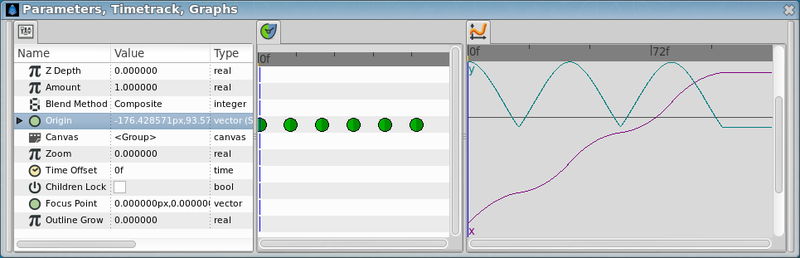
This coincides with the main waypoints of the last method we have seen. But look what's the result:
Its X movement graph looks ugly. It is not a straight line that means that the horizontal velocity is not constant. To solve that you have to insert more waypoints in the middle.
To do that I've uses the animation of the second method to try to match the position at regular intervals. This is the table I've needed.
| Time | Amount | Comments |
| 0f | 0.0 | Highest point |
| 20f | 0.2 | Lower point |
| 24f | 0.2626 | |
| 28f | 0.3085 | |
| 32f | 0.3463 | |
| 36f | 0.3741 | |
| 40f | 0.4 | Highest point |
| 44f | 0.4245 | |
| 48f | 0.4554 | |
| 52f | 0.4926 | |
| 56f | 0.5280 | |
| 60f | 0.6 | Lower point |
| 64f | 0.6629 | |
| 68f | 0.7075 | |
| 72f | 0.7445 | |
| 76f | 0.7783 | |
| 80f | 0.8 | Highest point |
| 84f | 0.8253 | |
| 88f | 0.8539 | |
| 92f | 0.8928 | |
| 96f | 0.9375 | |
| 100f | 1.0 | Lower point |
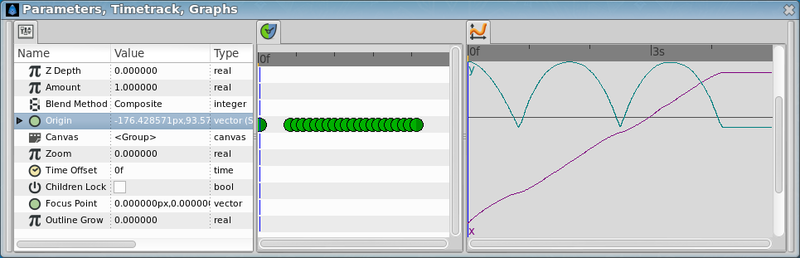
Now look to the graphs again and notice that the X travel is now a straight line.
This is the resulting animation and the sifz file.
The sample file: Media:bline.sifz
It is supposed that the small yellow ball should follow the red one all the time but you can see that is goes a little faster some times and a little slower other times. It is due to I need to use different times for the adjusting waypoints or add more of them.
Mathematical emulation
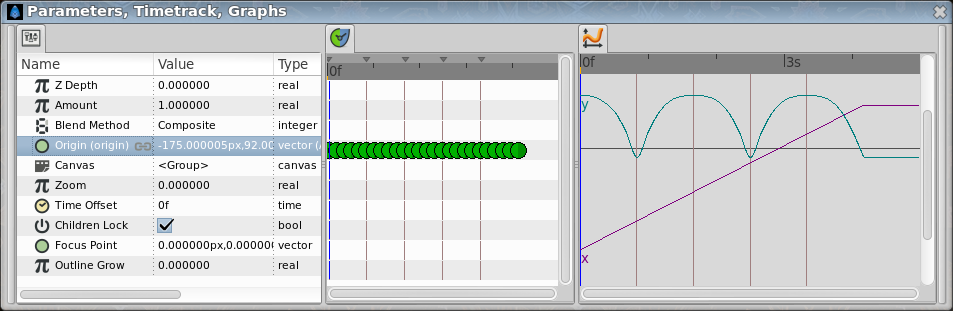
My approach is to imagine x and y movements as independent, so the x is simple (uniform rectilinear movement) and the y a little more complex. The first idea was to use the classical equations for acceleration (and gravity), but this would lead to need one equation per step (up-down or down-up). The ultimate idea is to use the sine function to describe the position at each timepoint, so... one equation would last forever!
Steps:
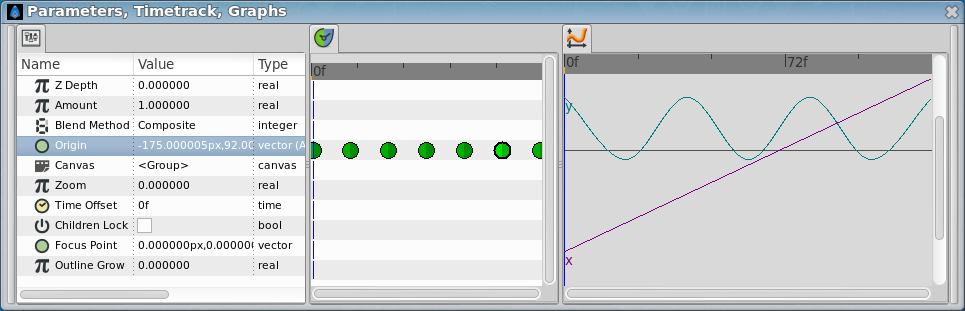
- Origin converted to composite
- X manualy animated to go linearly from left to right of the canvas: simple.
- Y converted to sine
- Sine Amplitude set to 1
- Sine DEG to time loop, and then:
- Timeloop link to 0 at 0 seconds and 180 at 1 second
- Timeloop duration: 1 second
- Rest timeloop parameters left to 0
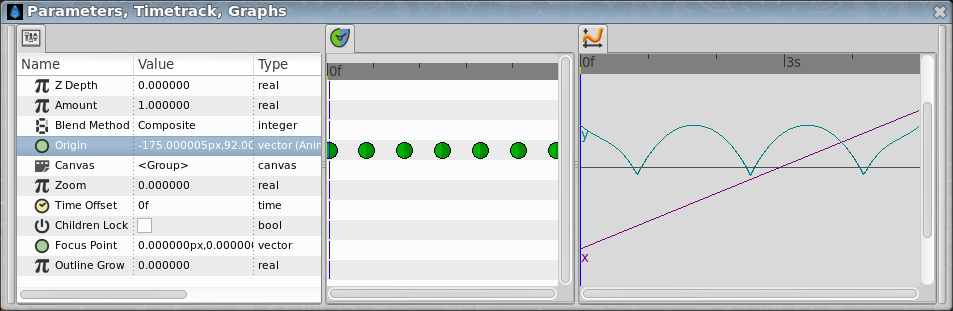
I guess the result is almost correct although the shape of the curve is not perfect, but I don't know why. Upgrades might make the effect better, such as the ball bouncing less each time with a more complex function.
Anyone want to try? :)
Conclusions
Traduit par --Ninchat 13:18, 20 November 2011 (UTC)