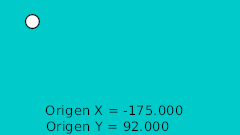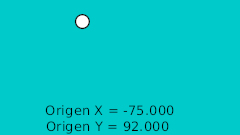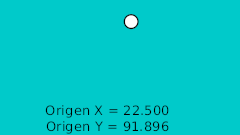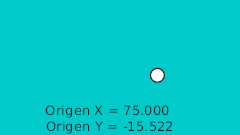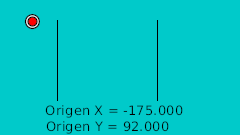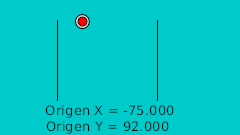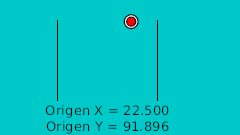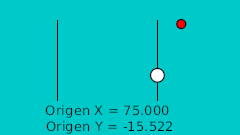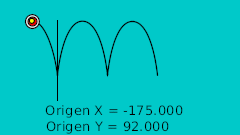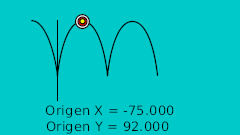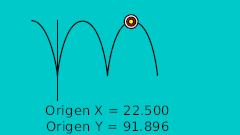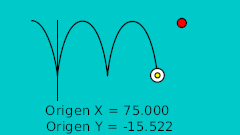Difference between revisions of "Doc:Ball Bounce/ru"

From Synfig Studio :: Documentation
Jump to: navigation, search
(→‎Ball Bounce following a path)
(@_@)
 
Line 152: Line 152:
 
Теперь можно двигать мяч и он будет всегда оставаться на кривой.
 
Теперь можно двигать мяч и он будет всегда оставаться на кривой.
  
−
Now expand the Origin parameter of the paste canvas layer of the encapsulated ball and search for the Amount parameter. This parameter is the one you need to animate to move the ball over the Bline.  
+
Раскройте параметры исходной точки вложенного слоя с мячом (нажав на треугольник напротив пункта "исходная точка") и найдите пункт "Величина", этот параметр как раз то что нам нужно для того чтобы анимировать движение вдоль кривой.
  
−
Considering the example, the bline has 6 vertices and 5 bline sections. If you are following the tutorial try to set that parameter to 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 and you will see that the ball moves to each vertex. Now create the following waypoints:
+
В нашем примере кривая Bline имеет 6 вершин и 5 секций кривой. Если вы в точности следуете примеру попробуйте установить величину на значения 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 и вы увидите что мяч двигается к каждой из вершин. Теперь создайте несколько фиксаторов:
  
 
{|  
 
{|  
−
| '''Time''' || '''Amount''' || '''Comments'''
+
| '''Время''' || '''Величина''' || '''Комментарий'''
 
|-  
 
|-  
−
| 0f || 0.0 || Highest point
+
| 0f || 0.0 || Высшая точка
 
|-  
 
|-  
−
| 20f || 0.2 || Lower point
+
| 20f || 0.2 || Низшая точка
 
|-
 
|-
−
| 40f || 0.4 || Highest point
+
| 40f || 0.4 || Высшая точка
 
|-  
 
|-  
−
| 60f || 0.6 || Lower point
+
| 60f || 0.6 || Низшая точка
 
|-  
 
|-  
−
| 80f || 0.8 || Highest point
+
| 80f || 0.8 || Высшая точка
 
|-  
 
|-  
−
| 100f || 1.0 || Lower point
+
| 100f || 1.0 || Низшая точка
 
|}
 
|}
  
−
This coincides with the main waypoints of the last method we have seen. But look what's the result:
+
Они соответствуют фиксаторам из предыдущего метода который мы разбирали, но посмотрите каков результат на этот раз:  
  
 
{{l|Image:bline-track.png|800px}}
 
{{l|Image:bline-track.png|800px}}
  
−
Its X movement graph looks ugly. It is not a straight line that means that the horizontal velocity is not constant. To solve that you have to insert more waypoints in the middle.  
+
График движения по X выглядит ужасно, это уже не прямая линия,а значит скорость движения по горизонтальной плоскости не является постоянной. Чтобы исправить это нужно добавить больше фиксаторов в середине.
  
−
To do that I've uses the animation of the second method to try to match the position at regular intervals. This is the table I've needed.
+
Чтобы сделать это я использовал анимацию из второго метода и постарался совместить положения мяча на всём протяжении кривой. Вот таблица которая мне понадобилась.
  
  
 
{|  
 
{|  
−
| '''Time''' || '''Amount''' || '''Comments'''
+
| '''Время''' || '''Величина''' || '''Коммнетарий'''
 
|-  
 
|-  
−
| 0f || 0.0 || Highest point
+
| 0f || 0.0 || Высшая точка
 
|-  
 
|-  
−
| 20f || 0.2 || Lower point
+
| 20f || 0.2 || Низшая точка
 
|-  
 
|-  
 
| 24f || 0.2626 ||  
 
| 24f || 0.2626 ||  
Line 196: Line 196:
 
| 36f || 0.3741 ||  
 
| 36f || 0.3741 ||  
 
|-
 
|-
−
| 40f || 0.4 || Highest point
+
| 40f || 0.4 || Высшая точка
 
|-  
 
|-  
 
| 44f || 0.4245 ||  
 
| 44f || 0.4245 ||  
Line 206: Line 206:
 
| 56f || 0.5280 ||  
 
| 56f || 0.5280 ||  
 
|-  
 
|-  
−
| 60f || 0.6 || Lower point
+
| 60f || 0.6 || Низшая точка
 
|-  
 
|-  
 
| 64f || 0.6629 ||  
 
| 64f || 0.6629 ||  
Line 216: Line 216:
 
| 76f || 0.7783 ||  
 
| 76f || 0.7783 ||  
 
|-  
 
|-  
−
| 80f || 0.8 || Highest point
+
| 80f || 0.8 || Высшая точка
 
|-  
 
|-  
 
| 84f || 0.8253 ||  
 
| 84f || 0.8253 ||  
Line 226: Line 226:
 
| 96f || 0.9375 ||  
 
| 96f || 0.9375 ||  
 
|-  
 
|-  
−
| 100f || 1.0 || Lower point
+
| 100f || 1.0 || Низшая точка
 
|}
 
|}
  
−
Now look to the graphs again and notice that the X travel is now a ''straight'' line.
+
Снова взглянув на график мы увидим что движение по X теперь равномерное и изображено ''прямой'' линией.
  
 
{{l|Image:bline-track2.png|800px}}
 
{{l|Image:bline-track2.png|800px}}
  
−
This is the resulting animation and the sifz file.  
+
Вот конечная анимация и файл .  
  
 
{{l|Image:bline.gif}}
 
{{l|Image:bline.gif}}
  
−
The sample file: {{l|Media:bline.sifz}}
+
Файл: {{l|Media:bline.sifz}}
  
−
It is supposed that the small yellow ball should follow the red one all the time but you can see that is goes a little faster some times and a little slower other times. It is due to I need to use different times for the adjusting waypoints or add more of them.
+
Предполагалось что маленький жёлтый мяч должен двигаться синхронно с красным на всём протяжении анимации, но как видите он движется быстрее или медленнее временами. Это произошло из за того что я был вынужден использовать фиксаторы не в одинаковых положениях времени или добавлять их в большем количестве.
  
 
== Mathematical emulation ==
 
== Mathematical emulation ==
  
 
Anyone want to try? :)
 
Anyone want to try? :)
−
 
−
==Conclusions==
 

Latest revision as of 11:07, 18 December 2012

Languages Language: 

English • español • français • русский

Warning!

This page contains outdated information.

The release of Synfig Studio 0.64.0 introduced new terminology and this translated page needs to be updated according to original English text.

You can help updating this page - see instructions here. Thank you!

warning end


В этой статье рассказывается о том как создать анимацию с прыгающим мячом. Мячи в мультиках обычно имеют достаточно причудливую форму когда двигаются и особенно когда ударяются об землю, но заниматься созданием таких деформаций мы будем в следующий раз, а сейчас рассмотрим способы создания самого движения мяча в пространстве.

Несколько разных способов достичь результата

Есть четыре способа создать прыгающий мяч используя Synfig:

  1. Сделать прыгающий мяч вручную, это потребует создания нескольких фиксаторов которые надо расположить так чтобы положение мяча совпадало с параболической траекторией его движения (во времени и пространстве).
  2. Используя параметр интерполяции фиксаторов, когда они установлены в режим TCB interpolation. Это значительно уменьшает количество необходимых фиксаторов и делает тайминг движения мяча на много проще.
  3. Используя привязывание к кривой, если вы нарисуете путь по которому должен двигаться мяч используя кривую BLine, то достаточно просто сделать так чтобы мяч следовал вдоль кривой и даже изменял свою скорость во время движения.
  4. Создать математическое уравнение описывающие движение мяча, это достаточно сложный способ но именно он должен оказаться самым точным из всех.

Создаём прыгающий мяч вручную

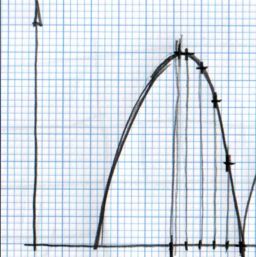
Принцип создания прыгающего мяча вручную заключается в том чтобы нарисовать желаемую кривую траектории на бумаге, а за тем прочертить от горизонтальной оси линии пересекающие кривую траектории с одинаковыми промежутками между собой. Примерно как на этом рисунке:

Bounce.jpg

Вы можете заметить что одинаковые промежутки на горизонтальной оси дают на вертикальной оси не одинаковые промежутки, это нормально так как проистекает из природы кривой.

Определив точки пересечения с кривой в двух измерениях мы можем перенести их в Synfig напрямую, используя для этого сетку. Нарисовав их мы исправляем значения координат так чтобы они были полностью симметричны, что наглядно показано в этой таблице:

Время Позиция X Позиция Y Комментарий
0f -175.0 92.0 Высшая точка
4f -165.0 92.0
8f -155.0 81.118
12f -145.0 63.678
16f -135.0 29.479
20f -125.0 -15.522 Низшая точка
24f -115.0 29.479
28f -105.0 63.782
... ...

Вы можете видеть что позиция Х возрастает с шагом в 10.0, а позиция Y воспроизводит параболическую траекторию кривой.

Чтобы получить большее количество прыжков просто скопируйте фиксаторы (поместите курсор на шкале времени в нужном месте, затем наведите мышь на фиксатор, нажмите правую кнопку мыши и выберите "продублировать") создав симметричное движение. Вам также придётся отредактировать значения Х вручную чтобы они возрастали на 10.0 на каждом новом фиксаторе.

Ниже вы можете видеть график созданного вручную движения мяча.

Manual-graph.png

Нижние точки графика не острые, чтобы исправить это нужно поместить большее количество фиксаторов в районе нижней точки (20f). Попробуйте сделать это сами с помощью приложенного файла с исходниками.

Ниже вы видите готовую анимацию и файл.

Image:manual.gif

File: Media:manual.sifz

Создаём прыгающий мяч с помощью интерполяции фиксаторов

В режиме интерполяции TCB мы можем изменять такие параметры фиксаторов как Натяжение, Непрерывность, Отклонение и Временное Натяжение, поэтому есть возможность легко изменять характер интерполяции в месте нахождения фиксатора делая его плавным или резким.

Сейчас мы возьмём те же значения для верхней и нижней точек что и в предыдущей таблице, но будем использовать только по одному фиксатору для каждой крайней точки, а оставшуюся часть кривой создадим с помощью TCB параметров.

Таблица фиксаторов будет выглядеть так:

Время Позиция X Позиция Y Комментарий
0f -175.0 92.0 Высшая точка
20f -125.0 -15.522 Низшая точка
40f -75.0 92.0 Высшая точка
60f -25.0 -15.522 Низшая точка
... ...

Как видите количество точек значительно уменьшилось.

Если просто использовать обычную TCB интерполяцию это не даст желаемый результат, посмотрите на график:

Waypoint-curves1.png

Но если изменить параметры TCB то мы получим то что хотели:

Waypoint-graph2.png


Параметры TCB должны быть такими:

Время Позиция X Позиция Y Комментарий Натяжение Непрерывность Отклонение Временное Натяжение
0f -175.0 92.0 Высшая точка 0.0 0.0 0.0 0.0
20f -125.0 -15.522 Низшая точка 0.0 -2.2 0.0 0.0
40f -75.0 92.0 Высшая точка 0.0 0.0 0.0 0.0
60f -25.0 -15.522 Низшая точка 0.0 -2.2 0.0 0.0
80f 25.0 92.0 Высшая точка 0.0 0.0 0.0 0.0
... ... ... ... ... ... ... ...


Вот анимация которую мы получили:

Image:waypoint-2.gif

И файл с исходниками file: Media:waypoint-2.sifz

Обратите внимание что кривая на 0 и 80 кадрах имеет не правильную форму, это произошло из за того что параметры TCB должны принадлежать к фиксатору находящемуся между двух других чтобы произвести эффект. Если фиксатор является крайним (находится в начале или конце анимации) то параметр не может изменять кривую. Чтобы решить эту проблему вам стоит разделить координаты X и Y Исходной Точки (Origin) изменив метод интерполяции для Y на линейный, а X оставить без изменений. Правильной ход анимации прыжка в примере по этой причине заключён между вертикальными чёрными линиями.

Заметьте также что вы можете сделать верхнюю точку более плоской увеличив параметр Временное Натяжение (хорошим значением будет 0.5). Это будет деформировать X так что вам нужно разделить координаты чтобы всё прошло гладко.

А это сравнение двух методов создания прыжка одновременно.

Image:waypoint-compare.gif

Используя этот метод вы можете легко изменять значение верхней точки Y, а интерполяция позаботится об остальном. При ручной интерполяции вам пришлось бы каждый раз пересчитывать все x/y координаты чтобы сделать высоту прыжка меньше.

Прыгающий мяч по кривой Bline

Перед тем как прочитать эту часть вам не помешает ознакомится со статьёй Doc:Following_a_BLine/ru.

Использования кривой для создания прыжка имеет следующие преимущества:

  • Вы можете сразу увидеть траекторию прыжка.
  • Вы можете вращать мяч во время движения (это позволяет сделать прыжки объектов не круглой формы).
  • Вы можете создать прыжки от вертикальной, горизонтальной и вообще какой угодно поверхности, только нарисуйте кривую.

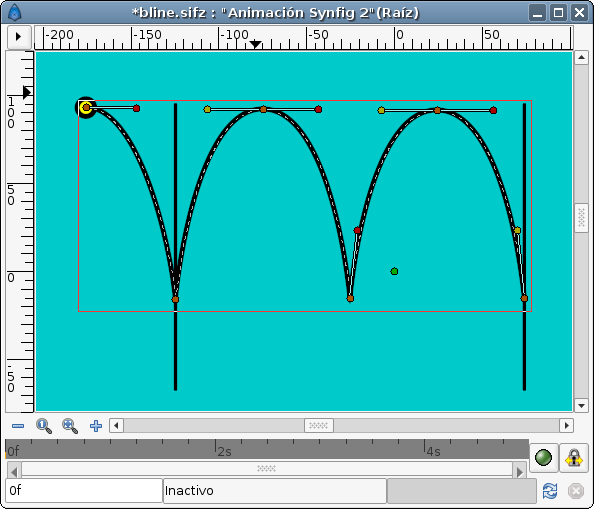
Первое что нужно сделать это нарисовать кривую вдоль которой будет двигаться мяч. Я рисовал кривую опираясь на анимацию созданного в ручную прыжка.

Image:bline-path.png

(Вы возможно заметили что не хватает некоторых касательных на кривой, не видно их по тому что я "связал" параллельные касательные острых краёв. Так гораздо проще настроить форму кривой потому что меняя положение только двух касательных вы двигаете все связанные касательные одновременно).

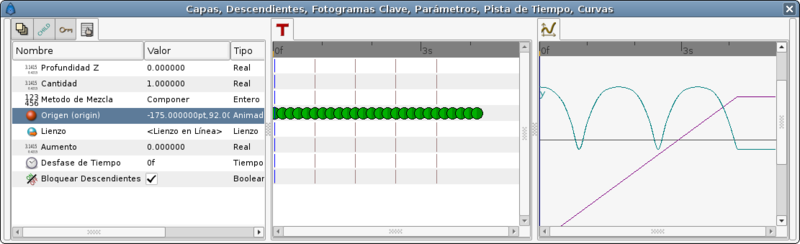
Теперь когда кривая нарисована нужно создать круг или мяч который будет прыгать и указать координаты исходной точки (origin) равными 0,0. Лучше всего изолировать мяч в объединяющий слой и использовать исходную точку объединяющего слоя для создания анимации. Когда создадите объединяющий слой надо выделить кривую которые вы нарисовали и объединяющий слой с мячём после чего выделить контрольную точку положения (зелёную) объединяющего слоя, потом кликнуть правой кнопкой на кривой (в месте где нет контрольных точек) и выбрать пункт "Привязать к кривой".

Теперь можно двигать мяч и он будет всегда оставаться на кривой.

Раскройте параметры исходной точки вложенного слоя с мячом (нажав на треугольник напротив пункта "исходная точка") и найдите пункт "Величина", этот параметр как раз то что нам нужно для того чтобы анимировать движение вдоль кривой.

В нашем примере кривая Bline имеет 6 вершин и 5 секций кривой. Если вы в точности следуете примеру попробуйте установить величину на значения 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 и вы увидите что мяч двигается к каждой из вершин. Теперь создайте несколько фиксаторов:

Время Величина Комментарий
0f 0.0 Высшая точка
20f 0.2 Низшая точка
40f 0.4 Высшая точка
60f 0.6 Низшая точка
80f 0.8 Высшая точка
100f 1.0 Низшая точка

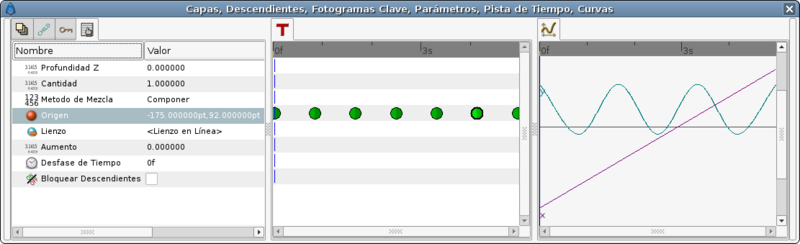
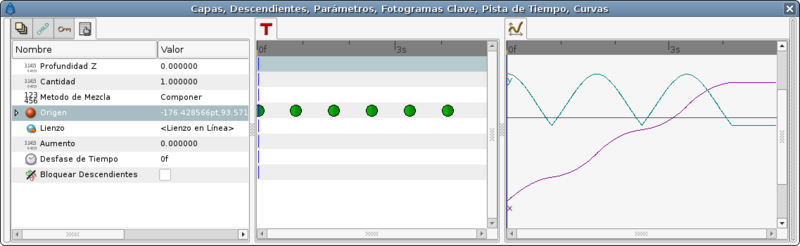
Они соответствуют фиксаторам из предыдущего метода который мы разбирали, но посмотрите каков результат на этот раз:

Bline-track.png

График движения по X выглядит ужасно, это уже не прямая линия,а значит скорость движения по горизонтальной плоскости не является постоянной. Чтобы исправить это нужно добавить больше фиксаторов в середине.

Чтобы сделать это я использовал анимацию из второго метода и постарался совместить положения мяча на всём протяжении кривой. Вот таблица которая мне понадобилась.


Время Величина Коммнетарий
0f 0.0 Высшая точка
20f 0.2 Низшая точка
24f 0.2626
28f 0.3085
32f 0.3463
36f 0.3741
40f 0.4 Высшая точка
44f 0.4245
48f 0.4554
52f 0.4926
56f 0.5280
60f 0.6 Низшая точка
64f 0.6629
68f 0.7075
72f 0.7445
76f 0.7783
80f 0.8 Высшая точка
84f 0.8253
88f 0.8539
92f 0.8928
96f 0.9375
100f 1.0 Низшая точка

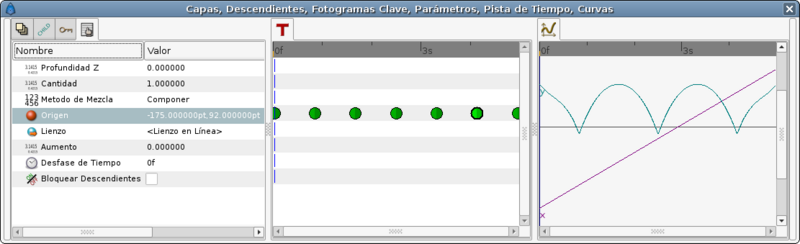
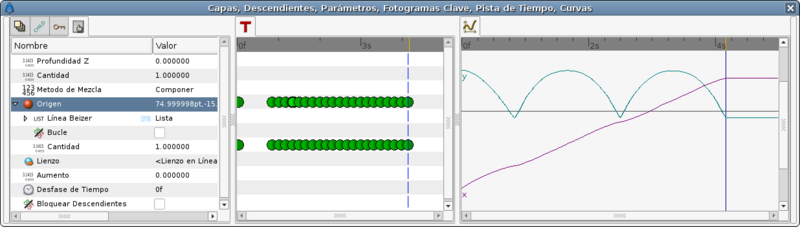
Снова взглянув на график мы увидим что движение по X теперь равномерное и изображено прямой линией.

Bline-track2.png

Вот конечная анимация и файл .

Image:bline.gif

Файл: Media:bline.sifz

Предполагалось что маленький жёлтый мяч должен двигаться синхронно с красным на всём протяжении анимации, но как видите он движется быстрее или медленнее временами. Это произошло из за того что я был вынужден использовать фиксаторы не в одинаковых положениях времени или добавлять их в большем количестве.

Mathematical emulation

Anyone want to try? :)


Languages Language: 

English • español • français • русский

Retrieved from "https://wiki.synfig.org/index.php?title=Doc:Ball_Bounce/ru&oldid=16533"